검색결과 리스트
글
SAT 수학 고득점멘토의 노하우+개념

[본 포스팅은 고우해커스 지구촌특파원 그린 님의 글을 재구성하여 작성했습니다]
SAT 수학 고득점멘토의 노하우+개념
안녕하세요 여러분 고우해커스입니다 !

오늘은 SAT 수학 영역에 대해서 더 자세히 설명하고 제가 자주 쓰는 노하우에 대해서 알려드리려고 합니다.
SAT 수학은 특히나 기본 개념이 너무나도 중요한 영역입니다.
SAT 수학 개념과 공식들을 알고 있어야 다양한 응용문제가 나왔을 때
당황하지 않고 아는 것을 활용해서 문제를 풀 수 있어야 합니다.
1. 용어
특히 한국에서 공부를 하던 분들은 SAT 수학 용어가 매우 중요한 것 같습니다.
한국어로 개념을 알아도 영어로 된 문제들을 풀 때 핵심 단어를 헷갈리면 아는 문제도
못 푸는 현상이 종종 일어나는 것 같아요.
문제가 무엇을 구하라고 하는지 이해를 일차적으로 해야 공식을 사용하던 말던 하니까요.
연습문제들을 풀면서 헷갈리는/모르는 단어들은 리딩 영역처럼 적어놓고 외우는 것을 추천드립니다.
Geometry에서는 도형과 각의 이름, 함수 이름/ 종류, 가장 기본적인 기울기 (slope) 절편 (intercept) 등등
문제를 이해하는데 중요한 핵심 단어가 되는 수학 용어들을 아는 게 중요합니다!
구글에 “대한수학회 수학 용어 사전”이라고 치면 사전이 나오는데 한글에서 영어로,
영어에서 한글로 양쪽으로 번역이 가능해서 매우 유용합니다!

2. 개념 정리
SAT 수학 영역에서는 총 24개의 subtopic들이 존재하는데 그게 무엇인지 알고 배우면서
개념 정리 노트를 적는 것을 추천드립니다. 이 SAT 수학 노트에는 문제를 푸는 방법,
옆에는 예시 문제 하나, 공식과 유의점들을 적어 놓고 계속 참고하면서 공부해 줬어요.
제가 썼던 노트 또한 공유하겠습니다! 여러분들도 개인이 노트를 만드는 게 제일 효과가 크지만 제 것을 쓰셔도 됩니다!
간단한 문제들도 개인의 노하우/ 팁이 생기면 시간을 정말 단축할 수 있습니다.

1. 그래프와 함수 매칭 (match the graph with the fuction)- 항상 y 절편을 먼저 찾습니다.
주로 기울기 보다는 한 눈에 파악할 수 있고 y=mx+b 의 형태로 나와있으면 바로 b를 확인 할 수 있어서
빠르게 틀린 답들을 표시합니다. y의 절편이 있는 보기들을 고른 후에 (주로 2개로 추릴 수 있습니다)
대입해서 답을 확인합니다.
2. 근의 합/곱 (the sum/product of solutions) - 은근 이차함수의 근의 곱/합이 뭐냐는
질문이 많이 나오는데 ax^2+bx+c 일때 합은 -b/a 곱은 c/a라는 것을 외우고 풀면
굳이 근을 일일이 구하지 않아도 합/곱을 빨리 구할 수 있습니다.

3. 2개의 일차함수가 근이 있는지 없는지 (the equations have no solution/one solution/infinite solution) -
근이 없으면 평행하는 선으로 기울기가 같아야합니다. 근이 한개만 있는 식들은 b^2 - 4ac = 0 을
이용해서 찾을 수 있습니다. 수 많은 근이 있으면 같은 함수임으로 2개의 식이 같게 만들어줍니다.
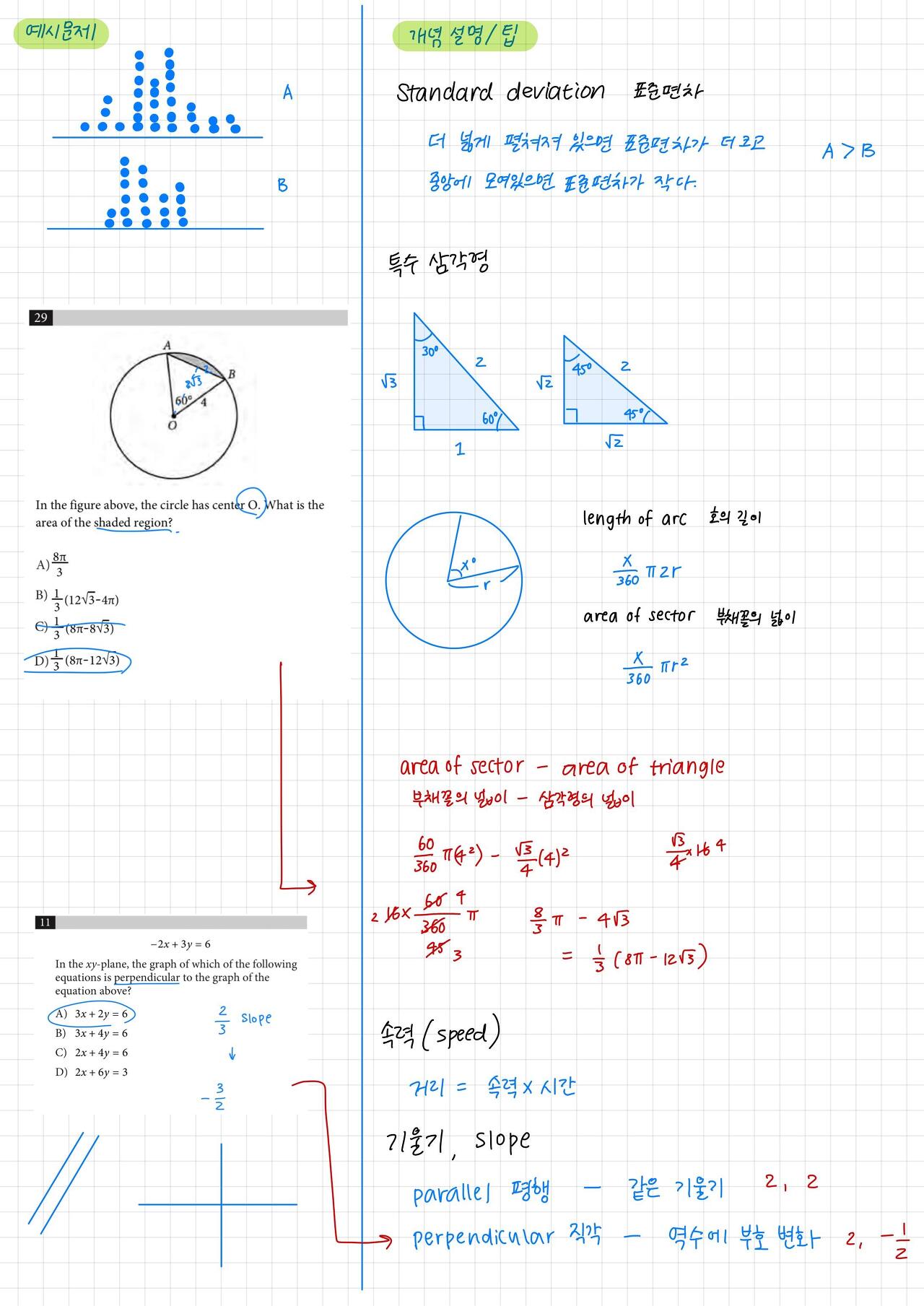
4. 표준편차 (standard deviation) - 숫자/ 데이터가 중앙으로 모여있으면 표준편차가
작고 흩어져 있으면 표준편차가 큽니다.

5. 그래프의 평균값/ 중앙값 - Mean / median on a graph - 정규분포 (대칭인 그래프)에서는
평균과 중앙값이 같습니다. 하지만 한 쪽으로 치우쳐져 있는 그래프들은 더 얄쌍한 (꼬리라고 흔히 얘기합니다)
쪽으로 평균값이 있습니다. 예를 들어 한 반의 시험 성적이 대체적으로 낮아서 0-60점 쪽에
데이터가 더 많고 60-100점에는 몇 명없는 그래프가 있다고 했을때 중앙값이 평균값보다 더 작을 것 입니다.
반대도 마찬가지로 60-100점에 더 많은 데이터가 있고 0-60점이 거의 없을때 중앙값은 평균값보다 더 큽니다.
6. 평균값/중앙값 - mean median with changing numbers - 가끔 나오는 유형인데
10개의 데이터가 있다고 했을때 숫자 중하나가 바뀌는 현상에 대해서 물어봅니다.
거의 제일 첫 아니면 마지막 숫자를 바꾸고 이럴때 중앙값은 각 숫자가 얼마인지랑은
상관없이 그냥 가운데 있는 숫자가 중요하기 때문에 중앙값은 바뀌지 않습니다.
하지만 평균은 각 숫자가 얼마인지가 중요하기 때문에 “변동이 있다”라고 알고 있으시면 됩니다.
7. 연립방정식 - Linear systems - 연립방정식이 나오고 x,y의 값을 물어보는 경우도 있지만
가끔은 3x+y 같은 어느 식의 값을 물어봅니다. 이럴때는 x와 y의 값을 각각 구해서 식에 대입할 수도 있지만
10번중 9번은 연립방정식을 그냥 더하면 값이 나오는 경우도 있습니다.
3. 시험을 잘 보는 방법
1. 푸는 속도를 조절하는게 중요해요. 문제를 많이 풀어본 학생들을
이미 많은 유형과 문제들을 접해봤기 때문에 빠르게 풀 수 있다는
과도한 자신감으로 너무 아까운 실수들을 하게 됩니다. 무슨 문제인지 아는 것 같아서 빠르게 접근 했다가
핵심 키워드를 놓치면서 문제를 틀리는 경우들도 있습니다. 반대로 시간 관리를
너무 안하고 느슨하게 풀다가 마지막에 몰아서 급하게 푸는 상황도 있을 수 있으니
시간에 유의 하면서 푸는 것이 중요합니다. 이렇게 시간에 영향을 받으면서
풀면 쉬운 SAT 수학 문제도 사소한 실수로 틀릴수 있습니다.

2. 암산은 금물, 조금이라도 적으면서 문제를 풀는 습관을 길르는게 중요해요.
문제를 머리로 풀기 시작하면 오류의 확률이 커집니다. 암산을 잘못하면서도
그 사실을 인지하지 못하면서 잘못된 답을 선택한체로 답지를 작성하게 됩니다.
또한 나중에 검산이나 복습을 할때 “내가 이 문제를 어떻게 풀었더라”가 확인이 안되면서
무엇이 틀렸는지 확인 할 수 없고 재확인 하는 시간이 더 오래듭니다.

3. 문제를 읽으면서 간략하게 필기하면서 풀기. SAT에서는 원어민이 봤을때도
긴 SAT 수학 문제들이 나올때가 많아요. 필요없는 설명이 들어가있거나
간단한 부분을 풀어서 줄글로 설명하면서 읽다보면 집중을 하기가 힘들때가 있어요.
그래서 꼭 읽으면서 문제에서 나오는 정보를 옆에 간략하게 적어가면서 문제를 풀면
더 머리 속이 정리가 더 잘되고 중요한 부분을 놓치지 않을 수 있습니다.
SAT 수학 문제를 가끔은 꼬아서 낼때도 있는데 x를 찾았다면 문제는 5x + 7의 값을
구하라 일 수도 있기 때문에 그런 부분들을 넘어가지 않으려면 적으면서 푸는게 가장 좋습니다.
▼아래 배너를 누르시면 고우해커스에서 더 많은 정보 확인이 가능합니다▼
'영어공부' 카테고리의 다른 글
| 아이엘츠 라이팅 Task 1, 2 작성요령! (0) | 2023.05.02 |
|---|---|
| SAT 시험일정 & 디지털 SAT 변동사항! (0) | 2023.04.25 |
| SAT 라이팅 문제유형분석! (ft.고득점 팁) (0) | 2023.04.17 |
| 아이엘츠 리스닝 점수 올리는 비법! (0) | 2023.04.14 |
| SAT 만점을 위한 마지막 복습방법 (0) | 2023.04.12 |




RECENT COMMENT